One Dimension: Length
 It is easy to measure the length of a straight line on a piece of paper using a ruler. Objects that can easily be measured in one dimension, like a line, are measured in inches. If something is longer we measure it in feet, yards or miles. These are the measurements we use every day, but they aren’t really that easy to use. We have to memorize that there are 12 inches in a foot, three feet in a yard, and 5,280 feet in a mile.
It is easy to measure the length of a straight line on a piece of paper using a ruler. Objects that can easily be measured in one dimension, like a line, are measured in inches. If something is longer we measure it in feet, yards or miles. These are the measurements we use every day, but they aren’t really that easy to use. We have to memorize that there are 12 inches in a foot, three feet in a yard, and 5,280 feet in a mile.
Scientists use a simpler measurement system called the metric system, where all the measurements are related to each other by a multiple of ten. The basic measurement in this system is called a meter (m). Use a tape measure to see how long 39 inches is; that’s the length of a meter. A centimeter (cm) is used to measure shorter lengths. There are 100 centimeters in a meter. (The prefix centi– in Latin means one hundred.) An even smaller measurement is a millimeter (mm), which is equal to the thickness of a dime. There are 10 millimeters in a centimeter and 1000 millimeters in a meter. Milli- means thousand in Latin. For long distances, the metric system uses a kilometer (km), which is exactly 1,000 meters. (This time the prefix, kilo-, comes from Greek and it also means a thousand.)
 Two Dimensions: Area
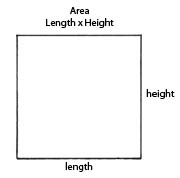
Two Dimensions: Area
It is a bit harder to calculate the dimensions of a square, isn’t it? The space inside a square (or other shape) is called area. To calculate area we need to take two measurements (you can remember this because a square is two-dimensional). Its area equals the length of its base times the length of its height. The units we use for area are typically in2 or cm2 (pronounced ‘square inches’ or ‘centimeters squared’). For example, if a square has sides that are 10 cm long, the area is 10 cm x 10 cm = 100 cm2.
Three Dimensions: Volume
For 3D objects, we calculate volume, which is how much total space the object takes up. To visualize what volume is, suppose you have a perfectly square container (length, width, and height all equal), and there is an opening at the top so you can pour water in. If you fill the container to the top, you will have a cube of liquid inside the container. The space the liquid takes up is the volume of the container. You could measure the amount of liquid in the cube to find the cube’s volume. The units of measurement for liquid volume are ounces, cups, quarts, and pints. In the metric system the standard measurement for liquid volume is a liter (l). Smaller amounts are measured in milliliters (ml). Remember that milli- means one thousand: there are 1000 milliliters in a liter. 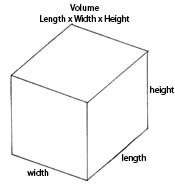
But what if the cube is solid? How can you measure its volume? You take three measurements (remember, a cube is three-dimensional) and multiply them together. Length x Width x Height = Volume. If the cube has sides 10 cm long, the volume would be 10 cm x 10 cm x 10 cm = 1000 cm3 (pronounced as cubic centimeters).
Here’s a convenient thing: 1 cm3 equals 1 ml of water. This means it is easy to compare liquid volume to solid volume. It also helps us measure irregular objects. If you have a rock, you can’t very well measure its length, width, and height—it’s not shaped like a cube! To find its volume, you can measure how much water it displaces. Put a rock in a cup of water and watch how the water level rises. This is because the rock takes up space and pushes the water out of the way. If you have a graduated cylinder, you can measure how much the water level moves up. If it moves up 25 ml, then you know the volume of the rock is equal to 25 ml of water. Since the rock is solid, we measure it in cubic centimeters, and since 1 cm3 equals 1 ml of water, we can figure out that the volume of the rock is 25 cm3.
Practice project:
- Determine the volume of a stick of butter in cm3 by measuring the length, width, and height and multiplying the three together. Write down your result.
- Unwrap the stick of butter and place it in a microwave-safe measuring cup. Microwave the butter on high for 45-60 seconds until it’s melted. You may have to stop the microwave and stir it a few times, to help it melt evenly.
- When it is completely melted, look at the markings on the measuring cup. Is the volume of the liquid butter the same as the volume of the block of solid butter? How did you determine that? (Hint: one 1/2 cup equals about 118 ml.)
Mass & Weight
There are two other important measurements scientists use often: mass and weight. On earth we measure mass (how much of a substance there is) by calculating weight (how heavy it is). The measurements are equal, so we tend to think of mass and weight as the same thing. But weight is dependent on how much gravity is pulling down on you. If you were to step on a scale on the moon, where there is less gravity, you would weigh less, but your body wouldn’t change in mass – there would still be as much of you as there is on earth. The standard unit of measurement for mass is a gram, which is a very small unit. One gram has about the same mass as a gummy bear.
A scale, like a spring scale or a diet scale, measures weight. It works because of the amount of gravity pulling the object down on the spring. A balance measures mass. On one side you put the object you want to measure, and on the other side you add something that you already know the mass of, like mass cubes or weights. When the two are equal, you know that the object has as much mass as what you put on the other pan.
Practice project: See how measuring mass works with a double-pan balance or a demonstration balance: put an apple in one pan, and in the other add 1 gram mass cubes (or masses from a mass set) until the two pans are balancing. Count how many mass cubes it took to equal the apple – that’s how much mass the apple has. (It’s also how much the apple weighs, since mass and weight are equal on Earth!)
Density
 Why do objects that are the same size sometimes have different weights? The answer has to do with their density. An object’s density is determined by comparing its mass to its volume. If you compare a rock and a cork that are the same size (they have equal volume), which is heavier? The rock is, because it has more mass. The rock is denser than the cork, then, because it has more mass packed into the same volume – this is due to the atomic structure of the elements, molecules, and compounds that make it up. To determine density, divide mass (g) by volume (ml). Your answer will be in grams per milliliter, g/ml. (Remember, you can measure the volume of an irregular solid object by seeing how many ml of water it displaces.)
Why do objects that are the same size sometimes have different weights? The answer has to do with their density. An object’s density is determined by comparing its mass to its volume. If you compare a rock and a cork that are the same size (they have equal volume), which is heavier? The rock is, because it has more mass. The rock is denser than the cork, then, because it has more mass packed into the same volume – this is due to the atomic structure of the elements, molecules, and compounds that make it up. To determine density, divide mass (g) by volume (ml). Your answer will be in grams per milliliter, g/ml. (Remember, you can measure the volume of an irregular solid object by seeing how many ml of water it displaces.)
Practice project: Solids aren’t the only things that have different densities. Try these experiments to learn about liquid density.





